Answer:
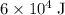 .
.
Step-by-step explanation:
KE lost = Total KE before Collision - Total KE after Collision.
For each car, the KE before collision can simply be found with the equation:
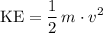 , where
, where
 is the mass of the car, and
is the mass of the car, and
 is the speed of the car.
is the speed of the car.
The
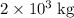 car would have an initial KE of:
car would have an initial KE of:
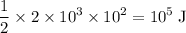 .
.
The
 car was initially not moving. Hence, its speed and kinetic energy would zero before the collision.
car was initially not moving. Hence, its speed and kinetic energy would zero before the collision.
To find the velocity of the two cars after the collision, apply the conservation of momentum.
The momentum
 of an object is equal to its mass
of an object is equal to its mass
 times its velocity
times its velocity
 . In other words,
. In other words,
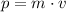 .
.
Let the mass of the two cars be denoted as
 and
and
 , and their initial speeds
, and their initial speeds
 and
and
 . Since the two cars are stuck to each other after the collision, their final speeds would be the same. Let that speed be denotes as
. Since the two cars are stuck to each other after the collision, their final speeds would be the same. Let that speed be denotes as
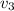 .
.
Initial momentum of the two-car system:
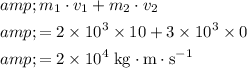 .
.
After the collision, both car would have a velocity of
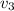 (since they were stuck to each other.) As a result, the final momentum of the two-car system would be:
(since they were stuck to each other.) As a result, the final momentum of the two-car system would be:
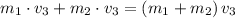 .
.
Since momentum is conserved during the collision, the momentum of the system after the collision would also be
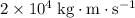 . That is:
. That is:
 .
.
Solve for
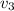 :
:
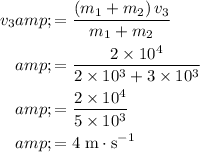 .
.
Hence, the total kinetic energy after the collision would be:
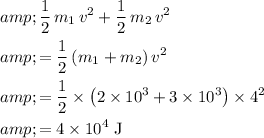 .
.
The amount of kinetic energy lost during the collision would be:
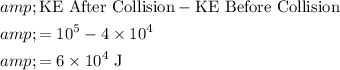 .
.