Question

A statistics student wants to compare his final exam score to his friend's final exam score from last year; however, the two exams were scored on different scales. Remembering what he learned about the advantages of Z scores, he asks his friend for the mean and standard deviation of her class on the exam, as well as her final exam score. Here is the information:

Answer 1

`z= (85-70)/(10)=1.5`

`z= (45-35)/(5)=2`

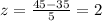
So then the correct answer for this case is:

B) Our student, Z= 1.50; his friend, Z=2.00.

Explanation:

Assuming this complete question:

A statistics student wants to compare his final exam score to his friend's final exam score from last year; however, the two exams were scored on different scales. Remembering what he learned about the advantages of Z scores, he asks his friend for the mean and standard deviation of her class on the exam, as well as her final exam score. Here is the information:

Our student: Final exam score = 85; Class: M = 70; SD = 10.

His friend: Final exam score = 45; Class: M = 35; SD = 5.

The Z score for the student and his friend are:

A) Our student, Z= -1.07; his friend, Z= -1.14.

B) Our student, Z= 1.50; his friend, Z=2.00.

C) Our student, Z= 1.07; his friend, Z= -1.14.

D) Our student, Z= 1.07; his friend, Z= 1.50

Step-by-step explanation:

Previous concepts

Normal distribution, is a "probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean".

The Z-score is "a numerical measurement used in statistics of a value's relationship to the mean (average) of a group of values, measured in terms of standard deviations from the mean".

Solution

Let X the random variable that represent the scores for our student, and for this case we know that:

`E(X)= \mu =70, SD_X=\sigma=10`

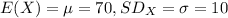
The z score is given by:

`z=(x-\mu)/(\sigma)`

If we use this we got:

`z= (85-70)/(10)=1.5`

Let Y the random variable that represent the scores for his friend, and for this case we know that:

`E(Y)= \mu =35, SD_Y=\sigma=5`

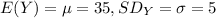
The z score is given by:

`z=(y-\mu)/(\sigma)`

If we use this we got:

`z= (45-35)/(5)=2`

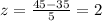
So then the correct answer for this case is:

B) Our student, Z= 1.50; his friend, Z=2.00.