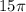Question:
The five circles making up this archery target have diameters of length 2,4,6,8, and 10. What is the total red area? Simplify your answer as much as you can.
The red area is provided in the image attached below:
Answer:
The total red area is
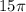
Step-by-step explanation:
It is given that the diameter of 5 circles making up the archery is 2,4,6,8, and 10.
To determine the total red area, we use the formula area of the circle =
 where radius
where radius
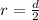
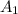 = Area of the 1st red circle =
= Area of the 1st red circle =
 =
=
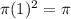
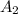 = Area of the 2nd white circle =
= Area of the 2nd white circle =
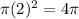
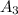 = Area of the 3rd red circle =
= Area of the 3rd red circle =
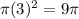
 = Area of the 4th white circle =
= Area of the 4th white circle =
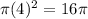
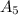 = Area of the 5th red circle =
= Area of the 5th red circle =
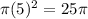
The total red area is given by
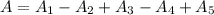
Substituting the values, we have,
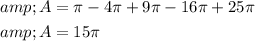
Thus, the total red area is