Answer:
Step-by-step explanation:
When the velocity of an object changes, it would experience an impulse. If the mass of the object stays the same, and that the object moves along a line, the value of the impulse
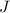 would be:
would be:
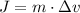 , where
, where
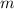 is the mass of the object, and
is the mass of the object, and
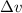 is the change in the velocity of the object.
is the change in the velocity of the object.
On the other hand, the change in the object's velocity can be found with the equation:
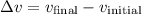 .
.
Note that if
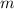 is in
is in
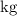 and
and
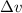 is in
is in
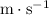 , the unit of
, the unit of
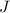 would be
would be
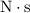 .
.
a.
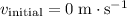 .
.
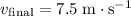 .
.
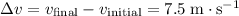 .
.
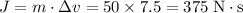 .
.
b.
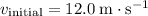 .
.
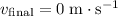 .
.
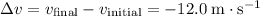
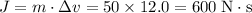 .
.
c.
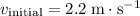 .
.
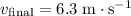 .
.
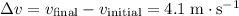 .
.
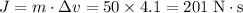 .
.
d.
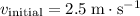 .
.
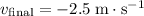 .
.
Note that
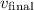 and
and
 are of opposite signs. The reason is that the object's velocity has changed direction in this period.
are of opposite signs. The reason is that the object's velocity has changed direction in this period.
 .
.
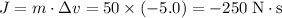 .
.