Answer:
a) Initial velocity = 0 m/s
b) Final velocity at ground = 21.7 m/s
Step-by-step explanation:
We consider only vertical motion for the required information.
The ball travels a vertical distance equal to the height of the building. See the attached file diagram.
At point A the initial velocity of the ball will be zero because it just starts from there. So
Initial velocity =Vi= 0 m/s
During its flight the ball travels a vertical distance equal to the height od the building.
Distance =S=24m
Gravitational acceleration = g= 9.8 m/sec2
Velocity at point B = Vf=?
Using
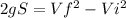
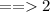 ×
×
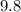 ×
×
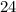 =
=
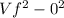
==>
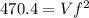
==> Vf =
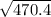
==> Vf= 21.7 m/sec
So the ball will hit the ground with 21.7 m/s velocity