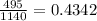Answer:
Explanation:
There are first 20 positive integers 1,2...20. Three distinct integers are chosen at random.
Total no of ways of drawing 3 integers =
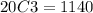
To Compute the probability that: (a) their sum is even
a) Sum can be even if either all 3 are even or 1 is even and 2 are odd.
There are in total 10 odd and 10 even.
Ways of sum even =
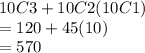
Prob =
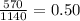
b) their product is even
Here any one should be even or both
SO no of ways are
=
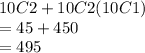
Prob =