Question

Bowie, age 52, has come to you for help in planning his retirement. He works for a bank, where he earns $60,000. Bowie would like to retire at age 62. He has consistently earned 8% on his investments and inflation has averaged 3%. Assuming he is expected to live until age 95 and he has a wage replacement ratio of 80%, how much will Bowie need to have accumulated as of the day he retires to adequately provide for his retirement lifestyle?

Answer 1

Bowie will require saving for $1,101,832.05 to achieve their goal.

Step-by-step explanation:

He expect to have wages 800% of what he currently owns:

60,000 x 80% = 48,000

Now, this will increase 3% per year for inflation reasons:

`Principal \: (1+ r)^(time) = Amount`

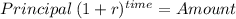
Principal 48,000.00

time 10.00

rate 0.03000

`48000 \: (1+ 0.03)^(10) = Amount`

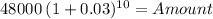
Amount 64,507.99

Now, we solve for the present value of an annuity of 33 year (95 - 62) with a real rate according to Irwin method of:

`(1+r_n)/(1+\theta ) -1 = r_r`

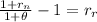
1.08/1.03 - 1 = 0.048543

`C * (1-(1+r)^(-time) )/(rate) = PV\\`

C 64,507.99

time 33

rate 0.048543

`64507.99 * (1-(1+0.048543)^(-33) )/(0.048543) = PV\\`

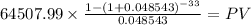
PV $1,101,832.0536