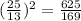Question

Completing the square:

find the value of c that completes the square.

1.) x
`x^(2) +6x+c`
2.)
`x^(2) -34x+c`
3.)
`x^(2) -(25)/(13) x+c`

Answer 1

Explanation:

Key to this method is remembering that

`(a+b)^2 = a^2 + 2ab + b^2`

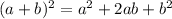
So, if you divide the coefficient of x by 2 and square it, that will complete the square. With that in mind, things are easy.

6/2 = 3, so add
`3^2 = 9`

`x^2+6x+9 = (x+3)^2`

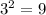
So, c=9

Similarly, for the other two,

`c = ((-34)/(2) )^2 = (-17)^2 = 289`

You don't really have to worry about the sign, since squaring will always make it positive

`((25)/(13)) ^2 = (625)/(169)`