Question

A 75 feet long conveyor is used at Home Depot to unload equipment from the truck to the platform. The

conveyor is med to an angle of elevation of 22
A What is the height from the truck to the platform (round to the nearest tenth)?
B. What is the length of the start of the conveyor to the end of the conveyor (round to the nearest
tent/?
C
M
the height of the truck to the platform is 37.5 feet, what must the angle of elevation be?​

Answer 1

A. height from truck to platform = 28 ft

B. length of the start of the conveyor to the end of the conveyor = 70 ft

C. If the height of the truck to the platform is 37.5 ft, the angle of elevation = 30°

Explanation:

Consider the sketch of the problem attached below.

based on the laws of trigonometry, we can recall that

sin θ =
`(opposite side of triangle )/(hypotenuse side of triangle)`

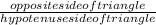
in this case, we are looking for the opposite side of the triangle.

hence we have, opposite side = 75 × sin 22

=28.095 ft ≈ 28 ft

as shown in the sketch, this opposite side is the height of the truck from hte platform

B Similarly, from the laws of trigonometry, the adjacent side of the triangle can be obtained using the relation

cos θ =
`(Adjacent side)/(Hypotenuse side)`

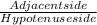
Adjacent side = hypotenuse side × cos θ

Adjacent side = 75 ×cos (22)

Adjacent side = 69.53 ≈ 70 ft

C. If the new height of the truck to the platform is now 37.5 feet, the problem is redrawn in sketch 2. However, the same formulas still apply.

Sin θ =
`(Opposite)/(Hypotenuse)`

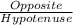
Sin θ =
`(37.5)/(75)` = 0.5

θ =
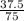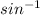`sin^(-1)` ( 0.5)

θ = 30°