Question

Ice cubes at 0°C with a total mass of 625 g are put in a microwave oven and heated with 750. W (750. J/s) of energy for 6.00 minutes. What is the final temperature of the water from the melted ice? Assume all of the microwave energy is absorbed by the ice/water and no heat loss by the ice/water. The enthalpy of fusion for ice is 6.02 kJ/mol and the heat capacity for water is 4.18 J/g･°C.

Answer 1

`T_f=23.34^(\circ)C`

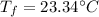
Step-by-step explanation:

Given:

initial temperature of the ice cube,
`T_i=0^(\circ)C`

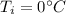
mass of the ice cube,
`m=625\ g`

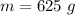
power of heating by the microwave oven,
`P=750\ W`

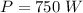
time duration of heating,
`t=6\ min=360\ s`

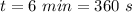
specific enthalpy of fusion of ice,
`L=6020\ J.mol^(-1)`

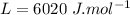
specific heat capacity of ice,
`c=4.18\ J.g^(-1)`

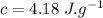
We find the energy supplied by the microwave:

`E=P.t`

`E=750* 360`

`E=270000\ J`

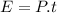
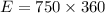
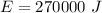
The energy required by the given mass of ice to melt:

`E_m=L*(m)/(M)`

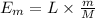
where:

M = molecular mass of the water

`E_m=6020* (625)/(18)`

`E_m=209027.78\ J`

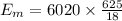
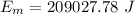
Remaining heat that is used in increasing the temperature of the melted ice i.e. water of 0°C:

`\Delta E=E-E_m`

`\Delta E=270000-209027.78`

`\Delta E=60972.22\ J`

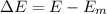
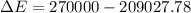
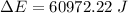
Now the rise in temperature of water:

From the heat equation,

`\Delta E=Q`

`\Delta E=m.c.(T_f-T_i)`

`60972.22=625* 4.18* (T_f-0)`

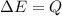
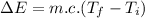
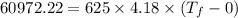
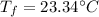`T_f=23.34^(\circ)C` is the final temperature of the water after the given heat input.

Answer 2

24°C

Step-by-step explanation:

m = Mass of ice = 625 g

Energy the microwave provides

`750* 6* 60=270000\ J`

Latent heat of melting = 334 J/g

Energy required to melt ice

`625* 334=208750\ J`

Actual energy

`270000-208750=61250\ J`

`C_s` = Heat capacity for water = 4.18 J/g･°C.

Energy required to melt ice will be equal to the heat absorbed

`Q=mC_s\Delta T\\\Rightarrow 61250=625* 4.18(T_f-0)\\\Rightarrow T_f=(61250)/(625* 4.18)+0\\\Rightarrow T_f=23.4449760766\ ^(\circ)C`

The temperature is 24°C