Answer:
58.7%
Explanation:
First, before calculating the braking efficiency of the car; we need to find the coefficient of the rolling friction of the driving by applying the formula;
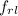
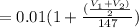
where;
V₁ = 90 mi/h
V₁ =
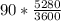 ( since 1 mi = 5280ft and 1 hour is equivalent to 3600 seconds)
( since 1 mi = 5280ft and 1 hour is equivalent to 3600 seconds)
V₁ =
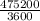
V₁ = 132
V₂ = 45 mi/h
V₂ =
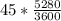
V₂ =
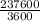
V₂ = 66
Substituting both data into the above equation, we have;
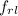
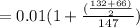
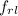
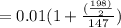
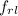

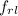
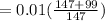
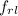
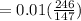
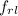
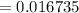
Now, to calculate the breaking efficiency of the car
 ; we apply the formula:
; we apply the formula:
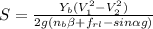
where;
the braking skid (S) = 410 ft
Value for braking mass factor for automobiles = 1.04
Value for Coefficient (β) of the road adhesion for both good and wet pavement = 0.90
Sin ∝ = 3% = 0.03
coefficient of the rolling friction
 = 0.016735
= 0.016735
V₁ = 132 & V₂ = 66
Substituting our parameters in the above formula, we have;
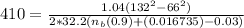
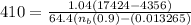
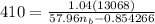
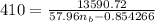

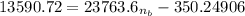
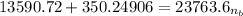
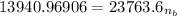
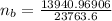
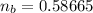
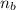 ≅ 0.587
≅ 0.587
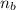 = 58.7%
= 58.7%
∴ The braking efficiency of the car = 58.7%