Answer:
5.739°
Explanation:
For the ship new angle bearing (β), since we are dealing with the second quarter and part of the third quater; we have β to be:
β= 240° - 90°
β= 150°
The question goes further by stating that the submarine shoots a torpedo traveling 5 times as fast as the ship.
i.e if the ship is = y
the submarine = 5y
∴ by sine rule which state that
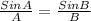 ; we can determine the angle that the submarine should fire the torpedo in order to hit the ship
; we can determine the angle that the submarine should fire the torpedo in order to hit the ship
∴ substituting our parameters; we have:
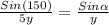
(Sin ∝) 5y = y × sin (150)
(Sin ∝) =
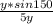
(Sin ∝) =
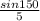
(Sin ∝) =
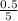
(Sin ∝) = 0.1
∝ = Sin⁻¹ 0.1
∝ = 5.739°
Thus, the angle that the submarine should fire the torpedo in order to hit the ship = 5.739°