Question

A proton is traveling horizontally to the right at 1.8 × 106 m/s. (a) Find the magnitude and direction of the weakest electric field that can bring the proton uniformly to rest over a distance of 3.20 cm? (b) How much time does it take the proton to stop after entering the field? (c) What minimum field (magnitude and direction) would be needed to stop an electron under the condition of part (a)?

Answer 1

528398.4375 N/C opposite to the direction of the proton

`3.56* 10^(-8)\ s`

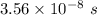
288.24609375 N/C in the same direction of the motion of the electron

Step-by-step explanation:

t = Time taken

u = Initial velocity = 0

v = Final velocity =
`1.8* 10^(6)\ m/s`

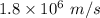
s = Displacement = 3.2 cm

a = Acceleration

Mass of electron =
`9.11* 10^(-31)\ kg`

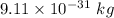
Mass of electron =
`1.67* 10^(-27)\ kg`

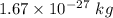
q = Charge of particle =
`1.6* 10^(-19)\ C`

`v^2-u^2=2as\\\Rightarrow a=(v^2-u^2)/(2s)\\\Rightarrow a=(0^2-(1.8* 10^6)^2)/(2* 0.032)\\\Rightarrow a=-5.0625* 10^(13)\ m/s^2`

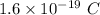
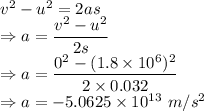
Electric field is given by

`E=(ma)/(q)\\\Rightarrow E=(1.67* 10^(-27)* -5.0625* 10^(13))/(1.6* 10^(-19))\\\Rightarrow E=−528398.4375\ N/C`

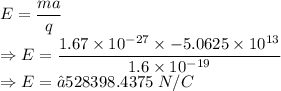
The electric field is 528398.4375 N/C opposite to the direction of the proton

`v=u+at\\\Rightarrow t=(v-u)/(a)\\\Rightarrow t=(0-1.8* 10^6)/(-5.0625* 10^(13))\\\Rightarrow t=3.56* 10^(-8)\ s`

The time taken is
`3.56* 10^(-8)\ s`

`E=(ma)/(q)\\\Rightarrow E=(9.11* 10^(-31)* -5.0625* 10^(13))/(-1.6* 10^(-19))\\\Rightarrow E=288.24609375\ N/C`

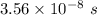
The electric field is 288.24609375 N/C in the same direction of the motion of the electron