Answer:
The area of the triangle is

Explanation:
Given:
Coordinates D (0, 0), E (1, 1)
Angle ∠DEF = 60°
△DEF is a Right triangle
To Find:
The area of the triangle
Solution:
The area of the triangle is =
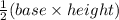
Here the base is Distance between D and E
calculation the distance using the distance formula, we get
DE =
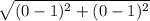
DE =

DE =
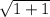
DE =

Base =

Height is DF
DF =
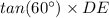
DF =
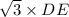
DF =
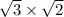
Now, the area of the triangle is
=
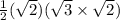
=

=
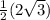
=
