Question

Assume a substance has a half-life of 19 years and the initial amount is 132 grams. How long will it be until only 35 % remains?

Answer 1

The answer to the question is

It will be ≅ 28.8 years until only 35 % of the substance remains

Step-by-step explanation:

To solve this we note the required relations and the given variables thus

The half life of the substance is

N(t) = N(0) ×
`((1)/(2) )^{\frac{t}{t_{(1)/(2) } } }`

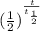
Thus when only 35% is remaining we have

35% of N(0) = N(0)×
`((1)/(2) )^{\frac{t}{t_{(1)/(2) } } }`

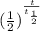
or 0.35 =
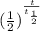`((1)/(2) )^{\frac{t}{t_{(1)/(2) } } }` , to solve the previous equation, we take the log of both sides thus

Log (0.35) = Log (
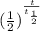`((1)/(2) )^{\frac{t}{t_{(1)/(2) } } }` ) or
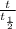`\frac{t}{t_{(1)/(2) } }`× log (1/2) =log(0.35)

⇒
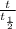`\frac{t}{t_{(1)/(2) } }` = 1.515 and since
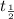`t_{(1)/(2) }` = 19 years we have

t = 19 × 1.515 = 28.776 Years

Therefore it will be 28.776 years before 35 % of the substance will be remaining