Question

An electric motor rotating a workshop grinding wheel at a rate of 120 rev/min is switched off. Assume constant angular deceleration of magnitude 1.94 rad/s 2 . How long does it take for the grinding wheel to stop? Answer in units of s.

Answer 1

Time taken t=6.614s

Step-by-step explanation:

Initial angular velocity ωi=120 rev/min= 12.5664 rad/s

Final angular velocity ωf=0

Angular acceleration a= -1.90 rad/s²

To find

Time taken

Solution

We can find time from angular velocity as:

Δω=at

`t=(w_(f)-w_(i) )/(a)\\t=(0-12.5664rad/s )/(-1.90rad/s^(2))\\ t=6.614s`

Answer 2

6.48s

Step-by-step explanation:

Angular acceleration/deceleration (α) is the time rate of change in angular velocity (ω). Mathematically,

α = Δω / t

α = (ω₂ - ω₁) / t ----------------------------(i)

where,

α = angular acceleration / deceleration

ω₂ = final angular velocity

ω₁ = initial angular velocity

t = time taken.

From the question,

α = angular deceleration = -1.94rad/s² (negative sign since its decelerating)

ω₂ = final angular velocity = 0 (since the grinding wheel comes to a stop)

ω₁ = initial angular velocity = 120rev/min

Convert 120rev/min to rad/s

Remember,

1 rev = 2π rad and

1 min = 60 s

=> 120rev/min =
`(120 rev)/(1 min)` =
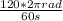`(120* 2\pi rad)/(60s)` = 12.5664rad/s

Substitute the values of α, ω₂ and ω₁ into equation (i)

=> -1.94 = (0 - 12.5664) / t

=> -1.94 = -12.5664 / t

Solving for t;

=> t = -12.5664 / -1.94

=> t = 6.48s

Therefore, the time it takes for the grinding to stop is 6.48s