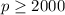Answer: c(p)= 0.18 p when
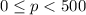
0.24 p when
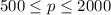
0.27 p when
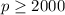
Explanation:
If p is the profit then and from the question we can relate as:
The 18% commission is for profits under $500
The 24% commission is for profits from $500 to $2,000
The 27% commission is for profits above $2,000
So, in terms of p, c(p) is given as:
c(p)= 0.18 p when
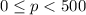
0.24 p when
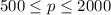
0.27 p when