Answer:
0.441296016722 m
Step-by-step explanation:
 = Initial speed =
= Initial speed =
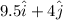
The magnitude of velocity is
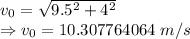
Take of angle
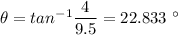
Range without halters

In this system the momentum is conserved
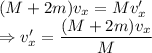
Change in velocity is given by
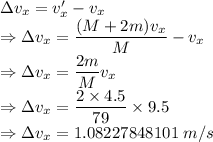
Time taken is

Difference in range is given by

The difference in range is 0.441296016722 m