Question

Determine whether each first-order differential equation is separable, linear, both, or neither.

dy/dx + e^x y = x^2 y^2

y + sin x = x^3 y'

In x - x^2 y = xy'

dy/dx + cos y = tan x

Answer 1

1.
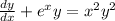`(dy)/(dx)+e^xy=x^2y^2`. It is not a first-order linear differential equation. And it's not separable either.

2.
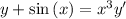`y+\sin \left(x\right)=x^3y'\:`. It is a first-order linear differential equation.

3.
`\ln \left(x\right)-x^2y=xy'\:`. It is a first-order linear differential equation.

4.
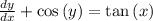`(dy)/(dx) +\cos \left(y\right)=\tan \left(x\right)`. It is not a first-order linear differential equation. And it's not separable either.

Explanation:

Definition 1: A first-order linear differential equation is one that can be put into the form

`(dy)/(dx) +P(x) y=Q(x)`

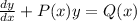
where P and Q are continuous functions on a given interval.

Definition 2: A first-order differential equation is said to be separable if, after solving it for the derivative,

`(dy)/(dx)=F(x,y)`,

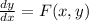the right-hand side can then be factored as “a formula of just x” times “a formula of just y”,

`F(x,y)=f(x)g(y)`

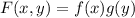
If this factoring is not possible, the equation is not separable.

Applying the above definitions, we get that

1. For
`(dy)/(dx)+e^xy=x^2y^2`

`(dy)/(dx)+e^xy=x^2y^2\\\\(dy)/(dx)=x^2y^2-e^xy\\\\(dy)/(dx)=y(x^2y-e^x)`

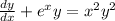
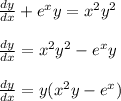
It is not a first-order linear differential equation. And it's not separable either.

2. For
`y+\sin \left(x\right)=x^3y'\:`

`x^3y'=y+\sin \left(x\right)\\\\x^3y'-y=\sin \left(x\right)\\\\y'\:-(1)/(x^3)y=(\sin \left(x\right))/(x^3)`

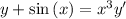
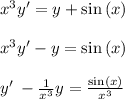
It is a first-order linear differential equation.

3. For
`\ln \left(x\right)-x^2y=xy'\:`

`xy'=\ln \left(x\right)-x^2y\\\\xy'+x^2y=\ln \left(x\right)\\\\y'\:+xy=(\ln \left(x\right))/(x)`

It is a first-order linear differential equation.

4. For
`(dy)/(dx) +\cos \left(y\right)=\tan \left(x\right)`

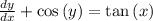
It is not a first-order linear differential equation. And it's not separable either.