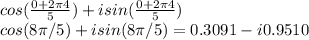Answer:
For K=0
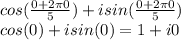
For K=1:

For K=2:

For K=3:
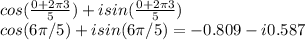
For K=4:
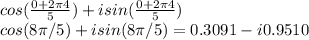
Explanation:
Fifth Root is given by:
![\sqrt[5]{z}=1+0i](https://img.qammunity.org/2021/formulas/mathematics/college/4avyzeenspxpu0mjdyu0bzoy0ix6wfhsri.png)
The above equation will become:
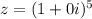
It can be written as:
![z=[cos(0)+isin(0)]^5](https://img.qammunity.org/2021/formulas/mathematics/college/gznzs3j3z47iawox5e86gngs8sf8qrcyru.png)
|z|=1,
According to De-moivre's Theorem:
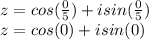
Now, Fifth Roots of unity in standard form a + bi :
![\sqrt[5]{z}=[{cos(0+2\pi k)+isin(0+2\pi k)}]^(1/5)](https://img.qammunity.org/2021/formulas/mathematics/college/s08d1zinfq8kba0ye6e4m98h6mz8ws5b7t.png)
k=0,1,2,3,4
For K=0
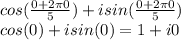
For K=1:

For K=2:

For K=3:
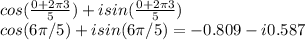
For K=4: