Question

For the points Upper P 1 (negative 3 comma 1 comma 5 )and Upper P 2 (1 comma 5 comma 0 )​, find the direction of ModifyingAbove Upper P 1 Upper P 2 with right arrow and the midpoint of line segment Upper P 1 Upper P 2.

Answer 1

The direction of
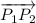`\overrightarrow{P_1P_2}` is (4,4,-5).

The midpoint of the line segment
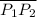`\overline{P_1P_2}` is in (-1 , 3 , 2.5)

Explanation:

The direction of a vector that goes from the initial point A to the final point B can be calculated as the subtraction of B with A. In this case:

`\overrightarrow{P_1P_2}=\vec{P_2}-\vec{P_1}=(1, 5, 0) - (-3, 1, 5)=(4, 4, -5)`

The midpoint of the line segment between two points A and B can be obtained as the halving of the addition of the vector A with the vector B. The line segment AB and the vector A+B make a rhombus. These lines will cross each other in their respective mediatrix. Therefore, if you obtain the point of the mediatrix of the vector A+B, you will find the midpoint of the segment AB. In this case:

`P_(mid1-2)=(\vec{P_1}+\vec{P_2})/2=(1)/(2)[(-3, 1, 5)+(1, 5, 0)]=(-1, 3, 2.5)`