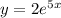Question

A curve passes through the point (0,2) and has the property that the slope of the curve at every point PP is five times the yy-coordinate of PP. What is the equation of the curve?

Answer 1

`y=2e^(5x)`

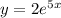
Explanation:

The slope of a curve is given by its derivative function. From the question, its value at any point (x, y) is 5 times y.

`(dy)/(dx)=5y`

`(dy)/(y)=5dx`

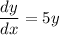
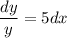
Integrate both sides

`\int(dy)/(y)=5dx`

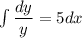
Don't forget the constant of integration

`\ln y= 5x + C`

`y=e^(5x+C)=e^(5x)\cdot e^C`

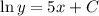
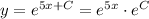
Since C is a constant, then
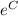`e^C` is constant. Let's call it A.

`y=Ae^(5x)`

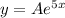
At the point (0, 2), when x = 0, y = 2.

`2=Ae^(5*0)`

`2=Ae^(0)`

`A=2`

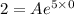
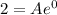
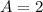
Hence,

`y=2e^(5x)`