Question

The sum of 2 numbers is 20. If we add to each number its square root, the product of both sums is 155.55. Find the two numbers with ǫ = 10−4

Answer 1

The two numbers are a = 13. 5 and b = 6.51

Explanation:

Data:

Let the two numbers be a and b respectively.

sum of two numbers is 20, so a + b = 20 ...1

sum plus square roots multiplied gives 155.55 so (a+√a) (b+√b) = 155.55 ...2

let f(y) = [20-b+√(20-b)]×[(b+√b)]-155.55 = 0

Multiplying out the terms gives;

f(y) = 20y-b²+20√b - b√b+b√(20-b)+√b·√(20-b) - 155.55 = 0

differentiating:

f'(y) =
`20-2y+(10)/(√(b) ) -((b)/(√(b) ) +√(b)) + (b)/(2√(20-b) ) +√(20-b) +(√(20-b) )/(2√(b) ) +(√(b) )/(2√(20-b) )`

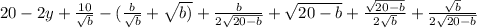
applying the Newton-Ralphson iteration method with the initial estimate of real zero roots gives P₀ = 10

That is
`P_(n+1) = P_(n) - (f(P_(n) )/(f'(P_(n)) )`

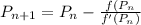
letting P₀ = 10 and iterating, the convergence occurs for b to 4 decimal places at P₇ = 6.51 = b

we also obtain from equation (1)

a + b = 20

a = 20 - b

a = 20 - 6.51

a = 13.5

Two numbers therefore are a= 13.5 and b = 6.51

Answer 2

see in given solution

Explanation: