Answer:
Option A:
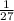
Explanation:
The first step to solve this exercise is to find the scale factor from the radius of the small sphere to the radius of the large sphere. This is:
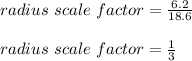
The second step is to find the scale factor from the volume of the small sphere to the volume of the large sphere. By definition, this will be:

Therefore, you must substitute the radius scale factor into the equation and then you must evaluate in order to find the volume scale factor. This is:
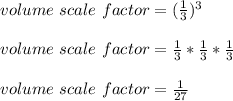
Then, the volume of the small sphere is
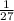 times the volume of the large sphere.
times the volume of the large sphere.