Question

In a quality control test of parts manufactured at Dabco Corporation, an engineer sampled parts produced on the first, second, and third shifts. The research study was designed to determine if the population proportion of good parts was the same for all three shifts. Sample data follow.

Production Shift


Quality first second third


Good 285 368 176


Defective 15 32 24


A. Using a .05 level of significance, conduct a hypothesis test to determine if the population proportion of good parts is the same for all three shifts. What is the p-value and what is your conclusion?


B. If the conclusion is that the population proportions are not all equal, use a multiple comparison procedure to determine how the shifts differ in terms of quality. What shift or shifts need to improve the quality of parts produced?

Answer 1

p value = 0.0174

Conclusion : we reject the null hypothesis

Explanation:

Thinking step:

We need to perform a test to determine if the proportion of the good parts is the same for all three shifts at a significance level of
`\alpha = 0.05`

Assumption : all the population for each or the three shifts is not equal.

Calculation:

Let p₁ be the sample of the first shift

p₂ be the sample of the second shift

p₃ be the sample of the third shift

According to the null hypothesis

H₀ = p₁ = p₂ = p₃

In other words, all the population sample proportions are equal.

Alternatively, we can assume that the three shift are not equal p₁ ≠ p₂ ≠ p₃

Tabulating and performing the
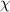`\chi`² test gives 8.10

degrees of freedom:

df = k - 1

= 3 - 1 = 2

Thus the degree of freedom is 2

Solving using the MINITAB software gives: p = 0.174

The solution shows that the p value < level of significance, then p-value lies in the range 0.0174≤
`\alpha`≤0.05

Therefore, we reject the null hypothesis based on the fact that the three shifts are not equal.