Question

On a coordinate plane, 2 lines are shown. Line A B has points (negative 4, negative 2) and (4, 4). Line C D has points (0, negative 3) and (4, 0).

Which statement best explains the relationship between lines AB and CD?


They are parallel because their slopes are equal.

They are parallel because their slopes are negative reciprocals.

They are not parallel because their slopes are not equal.

They are not parallel because their slopes are negative reciprocals

Answer 1

The first option

Explanation:

Just took the test and got it right

Answer 2

Option A) They are parallel because their slopes are equal.

Explanation:

We are given the following in the question:

Line AB:

(-4, -2), (4,4)

Line CD:

(0,-3), (4,0)

Formula to calculate slope =

`(x_1, y_1), (x_2, y_2)\\\\\\text{Slope} = m = (y_2 - y_1)/(x_2 - x_1)`

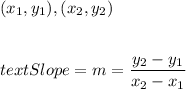
Slope of AB =

`(-4, -2), (4,4)\\\\m_(AB) = (4-(-2))/(4-(-4)) = (6)/(8) = (3)/(4)`

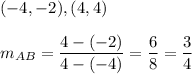
Slope of CD =

`(0,-3), (4,0)\\\\m_(CD) = (0-(-3))/(4-0) = (3)/(4)`

Thus,

`m_(AB) = m_(CD)`

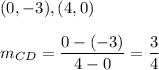
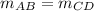
Thus, the two lines are parallel.

Option A) They are parallel because their slopes are equal.