Answer:
The area of the Patrick's building is
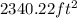 .
.
Explanation:
Shape of the Patrick's building = Decagon
In the figure attached:
Radius of the decagon = r = 12 feet
Side of the decagon = a
Angle AOB = 36°
Using trigonometric ratio is triangle AOC :
AO = r = 12 feet
AC =
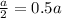
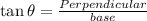
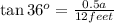
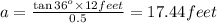
Area of decagon :
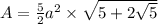
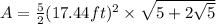
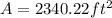
The area of the Patrick's building is
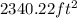 .
.