Question

A proton initially moves left to right along the x-axis at a speed of 2.00 x 103 m/s. It moves into an uniform electric field, which points in the negative x direction, and travels a distance of 0.200 m before coming to rest. If the proton's mass and charge are 1.67 x 10-27 kg and 1.60 x 10-19 C respectively, what is the magnitude of the electric field?

Answer 1

E = 1.04*10⁻¹ N/C

Step-by-step explanation:

Assuming no other forces acting on the proton than the electric field, as this is uniform, we can calculate the acceleration of the proton, with the following kinematic equation:

`vf^(2) -vo^(2) = 2*a*x`

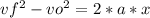
As the proton is coming at rest after travelling 0.200 m to the right, vf = 0, and x = 0.200 m.

Replacing this values in the equation above, we can solve for a, as follows:

`a = (vo^(2)*mp)/(2*x) = ((2.00e3m/s)^(2))/(2*0.2m) = 1e7 m/s2`

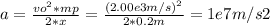
According to Newton´s 2nd Law, and applying the definition of an electric field, we can say the following:

F = mp*a = q*E

For a proton, we have the following values:

mp = 1.67*10⁻²⁷ kg

q = e = 1.6*10⁻¹⁹ C

So, we can solve for E (in magnitude) , as follows:

`E = (mp*a)/(e) =(1.67e-27kg*1e7m/s2)/(1.6e-19C) = 1.04e-1 N/C`

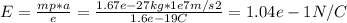
⇒ E = 1.04*10⁻¹ N/C