Question

Suppose that you are swimming in a river while a friend watches from the shore. In calm water, you swim at a speed of 1.25 m/s . The river has a current that runs at a speed of 1.00 m/s. Note that speed is the magnitude of the velocity vector. The velocity vector tells you both how fast something is moving and in which direction it is moving. If you are swimming upstream (i.a., against the current), at what speed does your friend on the shore see you moving?

Answer 1

Answer: The observing friend will the swimmer moving at a speed of 0.25 m/s.

Step-by-step explanation:

• Let S be the speed of the swimmer, given as 1.25 m/s

• Let
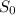  `S_(0)` be the speed of the river's current given as 1.00 m/s.

• Note that this speed is the magnitude of the velocity which is a vector quantity.

• The direction of the swimmer is upstream.

Hence the resultant velocity is given as,
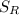`S_(R)` = S — S 0
`S_(0)`

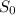
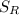`S_(R)` = 1.25 — 1

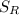`S_(R)` = 0.25 m/s.

Therefore, the observing friend will see the swimmer moving at a speed of 0.25 m/s due to resistance produced by the current of the river.