Question

Sebastian solved the radical equation y + 1 = but did not check his solution. (y + 1)2 = y2 + 2y + 1 = –2y – 3 y2 + 4y + 4 = 0 (y + 2)(y + 2) = 0 y = –2 Which is the true solution to the radical equation y + 1 = ? y = –2 y = 1 y = 2 There are no true solutions to the equation.

Answer 1

THE ANSWER IS D(there are no true solutions to the equation)

Answer 2

There are no true solutions to the equation.

Explanation:

The correct equation is

`y+1=√(-2y-3)`

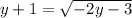
Solve for y

squared both sides

`(y+1)^2=(-2y-3)`

`(y^2+2y+1)=(-2y-3)`

`y^2+2y+1+2y+3=0`

`y^2+4y+4=0`

`(y+2)(y+2)=0`

`y=-2`

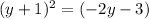
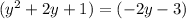
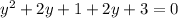
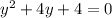
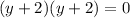
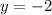
Verify

substitute the value of y in the original expression

`-2+1=√(-2(-2)-3)`

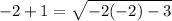
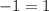`-1=1` ----> is not true

therefore

There are no true solutions to the equation.