Answer
given,
Length of the string, L = 2 m
speed of the wave , v = 50 m/s
string is stretched between two string
For the waves the nodes must be between the strings
the wavelength is given by
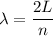
where n is the number of antinodes; n = 1,2,3,...
the frequency expression is given by

now, wavelength calculation
n = 1
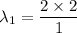
λ₁ = 4 m
n = 2

λ₂ = 2 m
n =3
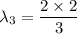
λ₃ = 1.333 m
now, frequency calculation
n = 1

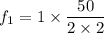
f₁ = 12.5 Hz
n = 2

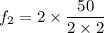
f₂= 25 Hz
n = 3

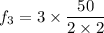
f₃ = 37.5 Hz