Question

There are 15 European cities that Kevin would eventually like to visit. On his next vacation, though, he only has time to visit 4 of the cities: one on Monday, one on Tuesday, one on Wednesday, and one on Thursday. He is now trying to make a schedule of which city he'll visit on which day. How many different schedules are possible?

Answer 1

32760 different schedules are possible.

Explanation:

The order is important.

For example

Prague on Monday, Berlin on Tuesday, Liverpool on Wednesday and Athens on Thursday is a different schedule than Berlin on Monday, Prague on Tuesday, Liverpool on Wednesday and Athens on Thursday.

So we use the permutations formula to solve this question.

Permutations formula:

The number of possible permutations of x elements from a set of n elements is given by the following formula:

`P_((n,x)) = (n!)/((n-x)!))`

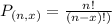
How many different schedules are possible?

Choose 4 cities among a set of 15. So

`P_((15,4)) = (15!)/((15-4)!)) = 32760`

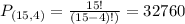
32760 different schedules are possible.