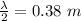Question

Two speakers, one directly behind the other, are each generating a 441-Hz sound wave. What is the smallest separation distance between the speakers that will produce destructive interference at a listener standing in front of them? Take the speed of sound to be 341 m/s.

Answer 1

Step-by-step explanation:

Given

Two speaker with frequency of
`f=441\ Hz`

Listener is standing in front of them

For destructive interference of sound waves i.e. when two waves with opposite signs of amplitude combines give destructive interference

for destructive interference path length difference is

`\Delta =|d_1-d_2|=(m+(1)/(2))\lambda`

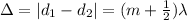
where
`\lambda =wavelength`

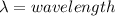
for
`m=0`

`\Delta =(\lambda )/(2)`

`velocity=frequency* wavelength`

`\lambda =(v)/(\\u )`

`\lambda =(341)/(441)=0.773\ m`

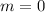
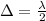
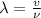
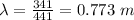
Smallest separation is
`(\lambda )/(2)=0.38\ m`