Answer:
X 2 3 4 5 6 7 8 9 10
P(X) 1/25 2/25 3/25 4/25 5/25 4/25 3/25 2/25 1/25
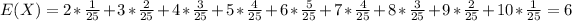
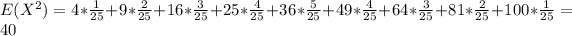
![Var(X) = E(X^2) -[E(X)]^2 = 40 -(6)^2 = 40-36 =4](https://img.qammunity.org/2021/formulas/mathematics/college/18dq6urdnhf47q2uy7s5gy9wde80i9coya.png)

Explanation:
For this case the possible values for the experiment on this case are:
(1,1) (1,2) (1,3) (1,4) (1,5)
(2,1) (2,2) (2,3) (2,4) (2,5)
(3,1) (3,2) (3,3) (3,4) (3,5)
(4,1) (4,2) (4,3) (4,4) (4,5)
(5,1) (5,2) (5,3) (5,4) (5,5)
And if we define the random variable X as the sum of two dice we have that the sample space is given by:
![S = [2,3,4,5,6,7,8,9,10]](https://img.qammunity.org/2021/formulas/mathematics/college/rd97mchcwzq91q4noig0g5q20iv9mk327l.png)
Now we can calculate the probability distribution counting calculating empirical probabilities and we have this distribution:
X 2 3 4 5 6 7 8 9 10
P(X) 1/25 2/25 3/25 4/25 5/25 4/25 3/25 2/25 1/25
And is verified that the sum of all the probabilities is 1.
The empirical probability for each case is calculated counting how many pairs represent an specific value for the sum divided by the 25 possibilities.
Now we can find the expected value with the following formula:
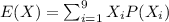
And if we replace we got:
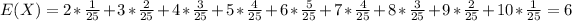
And for the standard deviation first we need to calculate the variance, and we can begin this calculating the expectation for the second moment given by:
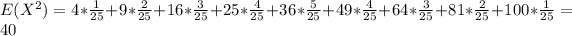
And the variance would be given by:
![Var(X) = E(X^2) -[E(X)]^2 = 40 -(6)^2 = 40-36 =4](https://img.qammunity.org/2021/formulas/mathematics/college/18dq6urdnhf47q2uy7s5gy9wde80i9coya.png)
And the deviation would be just the square root of the variance and we got:
