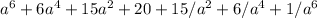Final answer:
The expansion of
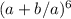 using the Binomial Theorem is
using the Binomial Theorem is
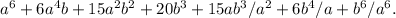 The coefficient of the
The coefficient of the
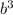 term is 20. If b = 1, the expression simplifies to
term is 20. If b = 1, the expression simplifies to
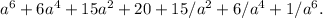
Step-by-step explanation:
To expand (a + b/a)^6 using the Binomial Theorem, we need to apply the formula which states that the expansion of (a + b)^n is:
an + nan-1b + n(n-1)an-262/2! + n(n-1)(n-2)an-363/3! + ...
Applying this formula, we get:
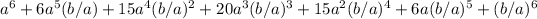
Simplifying, we have:
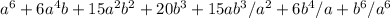
The coefficient of the
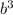 term is then 20.
term is then 20.
If we let b = 1, the expression simplifies to: