Question

Find f’(x). Compare the graphs of f and f’’ and use them to explain why your answer is reasonable.

f(x)=x4−2x3+x2

Answer 1

See the explanation below.

Explanation:

For this case we have the following function:

`y = f(x) = x^4 -2x^3 + x^2`

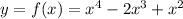
And we can find the first derivate and we got:

`y' = f'(x) = 4x^3 - 6x^2 + 2x`

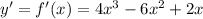
And we can take common factor x and we got:

`y' = f'(x) = x(4x^2 -6x+2)`

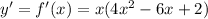
And for the second derivate we got:

`y'' = f''(x) = 12 x^2 - 12x +2`

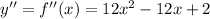
For this case we have the graph of the 3 functions in the figure attached.

The red line represent the original function, the blue one represent the first derivate and the green one the second derivate.

As we can see we have two points where we have a minimum for f(x) on this case (0,0) and (1.0), on these points the derivate function are equal to 0. If we analyze the function f(x) at point x=0.5 and we have that the value for this point correspond to (0.5, 0.0625).

We can see that when the function f(x) is increasing we see that f'(x) is positive and when the function is decreasing the derivate f'(x) is negative.

If we analyze the second derivate we see that for x=a, where:

`f''(a)>0` the function has a local minimum at x=a

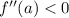`f''(a)< 0` the function has a local maximum at x=a

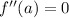`f''(a)=0` the function has a inflection point at x=a

As we can see for x=0.5 , f''(0.5)= -1 <0, for this reason we can conclude that 0.5 is a local maximum.

And for the inflection points x =0.211 and x=0.789 we have that
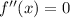`f''(x) =0` and these are points where the curvature of the function changes.