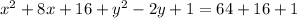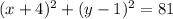Answer:
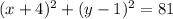
Explanation:
The standard of the equation of a circle is:
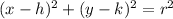 where point (h, k) is the center of the circle, and r is the radius of the circle.
where point (h, k) is the center of the circle, and r is the radius of the circle.
You need to complete the square for x and y.
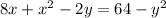
Move all variables to the left side by addition or subtraction.
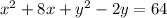
To complete a square, you need the square of half of the x or y term coefficient.
For x: 1/2 * 8 = 4; 4^2 = 16
For y: (1/2) * (-2) = -1; (-1)^2 = 1
We add 16 to complete the square in x and 1 to complete the square in x. We must add those numbers to both sides of the equation.