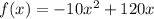Answer:
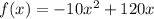
Explanation:
Let
x ----> the time in seconds
f(x) ----> the height in feet
we know that
The standard form for the quadratic, which is the function that models parabolic motion, is

Remember that
The problem tells us that the missile was launched from the ground, so c (the initial height of the missile) is 0.
so
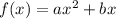
We have two given points
(1,110) and (2,200)
substitute
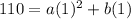
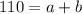 ----> equation A
----> equation A
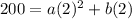
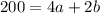 ----> equation B
----> equation B
Solve the system of equation s by graphing
Remember that the solution is the intersection point both lines
using a graphing tool
The solution is (-10,120)
see the attached figure
therefore
a=, b=
The quadratic equation is