Question

Referred to the triangle below what is the volume X. 44° (2x + 1) 98°

Answer 1

`$x=(53)/(2)^(\circ)`

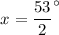
Solution:

Let us first define the exterior angle theorem of triangles.

Exterior angle theorem:

The measure of the exterior angle is equal to the sum of the measures of the two opposite interior angles.

In the given triangle,

Measure of exterior angle = 98°

Measure of one opposite interior angle = 44°

Measure of other opposite interior angle = (2x + 1)°

To find the value of x:

Using exterior angle theorem,

⇒ 44° + (2x + 1)° = 98°

⇒ 44° + 2x° + 1° = 98°

⇒ 45° + 2x° = 98°

⇒ 2x° = 98° – 45°

⇒ 2x° = 53°

`$\Rightarrow x=(53)/(2)^(\circ)`

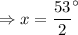
Hence the value of x is
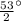`(53)/(2)^(\circ)`.