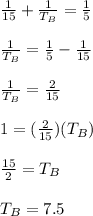Answer:
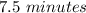
Explanation:
You need to apply the following formula:
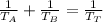
Where
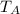 is the individual time for object A (In this case, cold water faucet),
is the individual time for object A (In this case, cold water faucet),
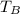 is the individual time for object B ( (In this case the hot water faucet) and
is the individual time for object B ( (In this case the hot water faucet) and
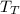 is the time for A and B together.
is the time for A and B together.
So, you can identify that:

Therefore, in order to find how long it will take for the hot water faucet to fill the tub on its own, you need to:
1. Substitute the known values into the formula.
2. Solve for
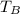 .
.
Therefore, you get the following result: