Question

A club consisting of 6 men and 8 women will choose a committee of 4. In how many ways

can the committee be chosen if it must contain at least 1 woman?
_

Answer 1

The number of ways the committee be chosen is 295 ways.

Explanation:

There are 6 men and 8 women.

A committee of 4, in which there must be at least 1 woman.

Let W- woman. M - man

So the combinations are: 1W, 3M or 2W, 2M or 3W, 1M or 4W

Now we have to use the combination formula and find the answer.

nCr =
`(n!)/(r!(n-r)!)`

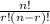
Using the above formula, we can find the answer.

4C1 × 7C3 + 4C2×7C2 + 4C3×7C1 + 4C4

=
`= (4!)/(1!(4-1)!) .(7!)/(3!(7-3)!) +(4!)/(2!(4 -2)!) .(7!)/(2!(7 -2)!) + (4!)/(3!(4 -3)!) .(7!)/(1!(7-1)!) +(4!)/(4!(4-4)!)`

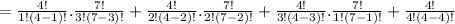
Simplifying the above factorials, we get

=4×35 + 6×21 + 4×7 + 1

= 140+126+28+1

= 295

The number of ways the committee be chosen is 295 ways.