Question

The volume of a 10 ounce box of cheerios is 258.75in3. the length of the box is 4 inches less than the height and the width is 3 inches. determine the height of the box

Answer 1

Height of the box = 11.5 in

Explanation:

Let h be the height of the box.

Assuming the volume of the Box is
`258.75\ in^3`.

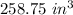Given:

Length = Height - 4 = h - 4

Width = 3 in

We need to find the height of the box.

Solution:

We know that the volume of the box.

`Volume = Length* height* width`

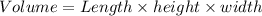
Substitute all given value in above formula.

`258.75 = (h-4)* h* 3`

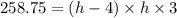
Rewrite the equation as:

`258.75 = 3h(h-4)`

`258.75 = 3h^2-12h`

`3h^2-12h-258.75=0`

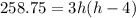
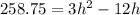
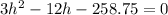
whole equation divided by 3.

`h^2-4h-86.25=0`

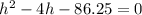
Use quadratic formula with
`a = 1, b = -4,c=-86.25`

`h=\frac{-b\pm \sqrt{(b)^(2)-4ac}}{2a}`

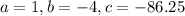
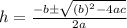
Put these a, b and c value in above equation.

`h=\frac{-(-4)\pm \sqrt{(-4)^(2)-4(1)(-86.25)}}{2(1)}`

`h=(4\pm √(16+345))/(2)`

`h=(4\pm √(361))/(2)`

`h=(4\pm 19)/(2)`

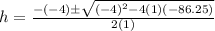
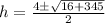
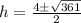
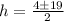
For positive sign

`h=(23)/(2)`

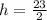
h = 11.5 in

For negative sign

`h=(-15)/(2)`

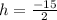
h = -7.5

We take positive value of h.

Therefore, the height of the box h = 11.5 in