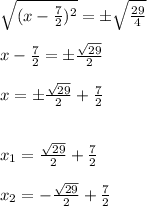Answer:
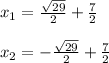
Explanation:
1. Subtract 9 from both sides of the equation:

2. Notice that the coefficient of "x" is 7. Then:
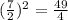
3. Add
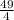 to both sides of the equation:
to both sides of the equation:
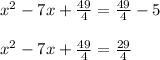
4. Completing the square, you get:
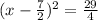
5. To find the solutions, you must square-root both sides of the equation, simplify, and solve for "x". Then, you get: