Question

1. Simplify. ((4x^4 y^5 )^4)/((4x^2 y^3 )^3 ) Show your work for each step.

Answer:



2. Solve for x. 〖(27)〗^(2y-2)=(3)^(2y+15)Show your work for each step.
Answer:

Answer 1

1.
`4x^(10)y^(11)`

2.
`y=5.25`

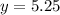
Explanation:

Question 1.

Given:

`((4x^4y^5)^4)/((4x^2y^3)^3)`

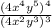
We need to Simplify given expression we get;

Solution:

Now we know that;

By Using Law of Indices which states;

`(x^m)^n=x^(m.n)`

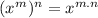
So we get:

`(4^4x^(4*4)y^(5*4))/(4^3x^(2*3)y^(3*3))\\\\(4^4x^(16)y^(20))/(4^3x^(6)y^(9))`

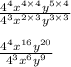
Now Again By Law of Indices we get;

`(x^a)/(x^b)=x^(a-b)`

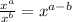
So we get:

`=4^((4-3))x^((16-6))y^((20-9))\\\\=4x^(10)y^(11)`

Hence Simplified expression is
`4x^(10)y^(11)`.

Question 2.

Given:

`(27)^((2y-2))=(3)^((2y+15))`

We need to solve for 'y'.

Solution:

To find 'y' we need to first make the base same.

Now we know that;

`27 = 3*3*3 = 3^3`

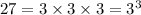
So we can say that:

`(3)^(3(2y-2))=(3)^(2y+15)`

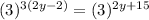
Now Applying Distributive property we get;

`(3)^(6y-6)=(3)^(2y+15)`

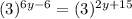
Now we can say that;

When an expression has equal bases then their exponent are said to equal too.

from above we get;

`6y-6=2y+15`

Combing like terms we get;

`6y-2y=15+6\\\\4y=21`

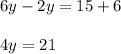
Dividing both side by 2 we get;

`(4y)/(4)=(21)/(4)\\\\y=5.25`

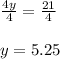
Hence The Value of y is 5.25.