Question

The measure of one angle of an octagon is two times smaller that of the other seven angles. What is the measure of each angle?

pls help the answer is (not 77 degrees and 144 degrees)

Answer 1

7 of the angles measure 144 degrees each and one angle measures 72 degrees

Explanation:

Let

x -----> represent the measures of the seven same-size angles,

x/2 ----> represent the measure of the one that is "two times smaller."

we know that

The sum of internal angles of a polygon can be calculated as:

`S=180^o(n-2)`

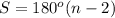
where

n is the number of sides of the polygon

In this case

n=8 (octagon)

substitute

`S=180^o(8-2)=1,080^o`

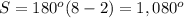
so

The linear equation that represent this problem is

`(x)/(2)+7x=1,080`

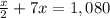
solve for x

`(15x)/(2)=1,080\\\\15x=2,160\\\\x=144^o`

so

`(x)/(2)=72^o`

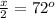
therefore

7 of the angles measure 144 degrees each and one angle measures 72 degrees