Question

What do the following two equations represent?
-4x-4y = -5
12x+12y = 112x

Answer 1

These two lines are parallel and system of these equations have no solution

Explanation:

Parallel Lines: Lines having same slope and different x and y intercept are parallel lines. System of such equations does not have any solution as these lines does not intersect at any finite points.

Standard form of line is
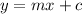`y=mx+c` where
`m` is slope and
`c` is y-intercept.

First Line:

`-4x-4y=-5\\\\-4y=-5+4x\\\\Divide\ both\ sides\ by\ -4\\\\y=-x+(5)/(4)\\\\compare\ with\ y=mx+c\\\\slope=-1,\ c=(5)/(4)`

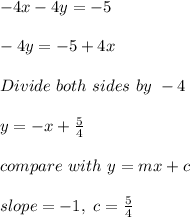
Second Line:

`12x+12y=112\\\\12y=112+-12x\\\\Divide\ both\ sides\ by\ 12\\\\y=-x+(12)/(112)\\\\compare\ with\ y=mx+c\\\\slope=-1,\ c=(12)/(112)`

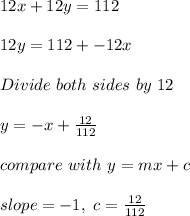
Hence these two lines are parallel and system of these equations have no solution