Answer:
Area of rectangle is

Perimeter of Rectangle is
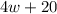 .
.
Explanation:
Given:
Let the width of the rectangle be 'w'.
Also Given:
A rectangle has a length that is 5 meters greater than the width.
Length of rectangle =
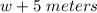
We need to write expression for Area of rectangle and Perimeter of rectangle.
Solution:
Now we know that;
Perimeter of rectangle is equal to twice the sum of the length and width.
framing in equation form we get;
Perimeter of rectangle =

Also We know that;
Area of rectangle is length times width.
framing in equation form we get;
Area of rectangle=
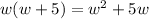
Hence Area of rectangle is
 and Perimeter of Rectangle is
and Perimeter of Rectangle is
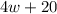 .
.