Question

A rectangle is formed from a square by adding 6 m to one side and 3 m to the other side. The area of the rectangle is 238 m². Find the dimensions of the original square.

Answer 1

11 meter

Explanation:

Given: A rectangle is formed from a square by adding 6 m to one side and 3 m to the other side.

The area of the rectangle is 238 m².

Now, finding the dimension of the original square.

Lets assume the side of square be "s".

∴ Width=
`s+6`

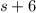
Length=
`s+3`

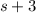
We know, area of rectangle=
`width* length`

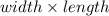
Subtituting the value in the formula to find the dimension or side of square.

⇒

using distributive property of multiplication.

⇒
`238= s^(2) + 3s+6s+18`

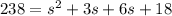
Subtracting both side by 238

⇒
`s^(2) + 9s-220= 0`

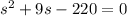
Solving by using quadratic formula to find value of s.

Formula:
`\frac{-b\pm \sqrt{b^(2)-4(ac) } }{2a}`

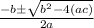
∴ In the expression
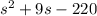`s^(2) +9s-220`, we have a= 1, b= 9 and c= -220.

Now, subtituting the value in the formula.

=
`\frac{-9\pm \sqrt{9^(2)-4(1*-220) } }{2*1}`

=
`(-9\pm √(81-4(-220) ) )/(2)`

=
`(-9\pm √(81+880 ) )/(2)`

=
`(-9\pm 31 )/(2)`

=
`(-40)/(2) or\ (22)/(2)`

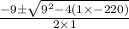
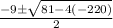
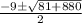
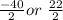
= -20 or 11

Ignoring negative result as dimension cannot be negative.

∴ The dimension of square will be 11 meter.

Answer 2

Therefore,

Dimensions of the Original Square is

`x =11\ m`

Explanation:

Given:

Let the side of Square be "x" meter

Then the Dimensions of a Rectangle is formed by adding 6 m to one side and 3 m to the other side wil be.

`Length = x+6\\\\Width=x+3`

Area of Rectangle =238 m²

To Find:

x = ? (Dimension of Original Square)

Solution:

Area of Rectangle is given by

`\textrm{Area of Rectangle}=Length* Width`

Substituting the values we get

`238=(x+6)* (x+3)`

Opening the Parenthesis we get

`238=x^(2)+9x+18\\\\x^(2)+9x+-220=0` ......Which is Quadratic equation

On Factorizing and Splitting the middle term we get

`x^(2)+20x-11x-220=0\\\\x(x+20)-11(x+20)=0\\\\(x+20)(x-11)=0\\\\x+20=0\ or\ x-11=0\\\\x=-20\ or\ x=11`

As distance cannot be negative therefore,

`x =11`

Therefore,

Dimensions of the Original Square is

`x =11\ m`