Question

The perimeter of the rectangle is 22 meters, and the perimeter of the triangle is 12 meters. Find the dimensions of the rectangle.

Answer 1

Length:8 m

Width:3 m

Explanation:

The complete question is

If the perimeter of a rectangle is 22 meters, and the perimeter of a right triangle is 12 meters (the sides of the triangle are half the length of the rectangle, the width of the rectangle, and the hypotenuse is 5 meters). How do you solve for L and W, the dimensions of the rectangle.

step 1

Perimeter of rectangle

we know that

The perimeter of rectangle is equal to

`P=2(L+W)`

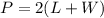
we have

`P=22\ m`

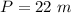
so

`22=2(L+W)`

Simplify

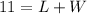`11=L+W` -----> equation A

step 2

Perimeter of triangle

The perimeter of triangle is equal to

`P=(L)/(2)+W+5`

`P=12\ m`

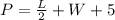
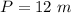
so

`12=(L)/(2)+W+5`

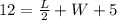
Multiply by 2 both sides

`24=L+2W+10`

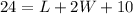
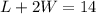`L+2W=14` ----> equation B

Solve the system of equations by graphing

Remember that the solution is the intersection point both graphs

using a graphing tool

The solution is the point (8,3)

see the attached figure

therefore

The dimensions of the rectangle are

Length:8 m

Width:3 m