Answer:
a) y√10
b) y√3
Explanation:
The opposite of square root is squaring a number. Opposite cancel each other out:
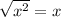
If you can't cancel everything out, you would leave the other numbers inside the root:
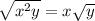
a)
√(10y²)
= √10 √y² Apply the root to each number
= y√10 √y² cancelled out to y
Since 10 had no "double" factors, it can't be further simplified.
To find "double" factors, find prime factors of 10:
10 = 5 X 2
There are no repeated factors, so you leave 10 under the root.
b)
√(3y²)
= √3 √y² Apply the root to each number
= y√3 √y² cancelled out to y
3 also does not have "double" factors.
3 = 3 X 1
Neither 3 nor 1 are square numbers.